| Voir le sujet précédent :: Voir le sujet suivant |
| Auteur |
Message |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 06/09/2013 18:41 Sujet du message: Tracer un couple elliptique? Posté le: 06/09/2013 18:41 Sujet du message: Tracer un couple elliptique? |
  |
|
|
bonsoir à tous,
J'ai téléchargé un plan de planeur dont les couples sont elliptiques.
La qualité du dessin n'étant pas fameuse, j'ai envie de redessiner les couples, or ceux-ci ont une forme semi-elliptique.
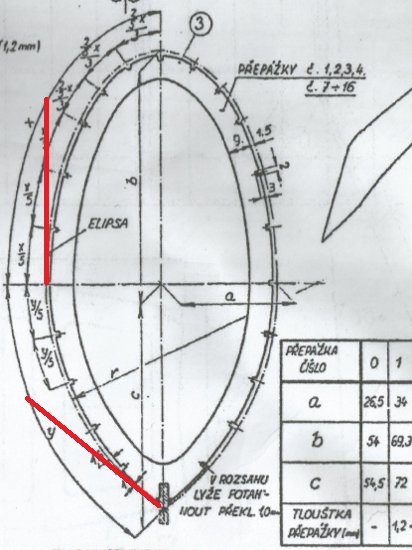
Pour la partie haute du couple, ça ne devrait pas poser trop de problème (un tableau donne les valeurs a et b). Pour la partie basse, il me semble qu'il s'agit d'un arc de cercle (de rayon r), mais son centre n'est pas indiqué, à part le fait qu'il se situe en-dehors du couple...
Comment tracer la partie inférieure? Je pensais mesurer l'angle que fait le bas du couple avec l'axe vertical, et venir faire tangenter l'arc de cercle avec les deux droites en rouge.
Tout ça me paraît bien compliqué, j'ai dû passer à côté de quelque chose de plus simple...

Fabrice |
|
| Revenir en haut de page |
|
 |
VincentB
Serial Posteur


Inscrit le: 23 Jan 2006

Localisation: Lanzarote - Charco del Palo
Âge: 62

|
 Posté le: 06/09/2013 18:52 Sujet du message: Posté le: 06/09/2013 18:52 Sujet du message: |
  |
|
|
Salut Fabrice,
j'ai pas bien compris, si t'as toutes les données de rayons.... ![[humm]](images/smiles/humm.gif)
mais perso, je ne m'embêterais pas avec les rayons et tout ça, je repasserais le contour du couple à la spline, que ce soit bien harmonieux à l'oeil, repassage de la spline à la polyligne et mise à l'echelle des différents couples. C'est un antik ou une maquette?

Retroplane et modélisme en pause, vanlife à haute dose. |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 06/09/2013 19:05 Sujet du message: Posté le: 06/09/2013 19:05 Sujet du message: |
  |
|
|
Je ne possède pas la valeur de r, c'est là qu'est l'os! 
Oui, le coupe de la spline, pourquoi pas.
Sinon, c'est un antique, mais pas pour tout de suite, je suis sur un projet plus... aquatique.

Fabrice |
|
| Revenir en haut de page |
|
 |
ClaudeL
Accro Posteur


Inscrit le: 26 Jan 2006

Localisation: Vercors (FR)
Âge: 78

|
 Posté le: 06/09/2013 22:03 Sujet du message: Posté le: 06/09/2013 22:03 Sujet du message: |
  |
|
|
Fabrice,
Tu peux mesurer r, a et c sur le dessin initial (avec un double décimètre) puis avec deux règles de trois tu calcules 2 valeurs de r à partir des valeurs de a et de c : les deux valeurs doivent être proches.  |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 07/09/2013 07:12 Sujet du message: Posté le: 07/09/2013 07:12 Sujet du message: |
  |
|
|
Oui, Claude, je suis d'accord.
Je cherchais davantage une méthode mathématique pour le tracé!
Des nouvelles... dans quelque temps. 

Fabrice |
|
| Revenir en haut de page |
|
 |
VincentB
Serial Posteur


Inscrit le: 23 Jan 2006

Localisation: Lanzarote - Charco del Palo
Âge: 62

|
 Posté le: 07/09/2013 07:44 Sujet du message: Posté le: 07/09/2013 07:44 Sujet du message: |
  |
|
|
Y'a 2 méthodes, le tracé de l'ingénieur et le tracé de l'ouvrier qui cintre un couvre-joint pour dessiner toutes ses courbes 

Retroplane et modélisme en pause, vanlife à haute dose. |
|
| Revenir en haut de page |
|
 |
jean claude Crétal
Serial Posteur


Inscrit le: 21 Avr 2008

Localisation: Charente-Maritime
|
 Posté le: 07/09/2013 07:52 Sujet du message: Posté le: 07/09/2013 07:52 Sujet du message: |
  |
|
|
Bonjour Fabrice si tu as gardé un bouquin de tables mathématique avec la flèche et la corde tu dois trouver le rayon.
Sinon la méthode géométrique: par 3 points il ne passe qu'un cercle.
tu détermines un point au milieu de ton arc tu imagines les 2 segments, les bissectrices des deux segments vont se croiser au centre du cercle.
Ça se trace avec un compas.
Ce n'est peut être pas très clair mais bon je sors du lit et je suis en vacances et pas de scan pour éclairer le texte 

Jean-Claude
"Si il n'y avait pas le sol, l'Aviation ça serait pas dangereux!!!..."
Marcel Jeanjean (sous les cocardes 1919) |
|
| Revenir en haut de page |
|
 |
Anonyme
Serial Posteur


Inscrit le: 26 Jan 2006

|
|
| Revenir en haut de page |
|
 |
Frédéric
Psycho Posteur


Inscrit le: 22 Juin 2006

Localisation: Corrèze
Âge: 61

|
 Posté le: 07/09/2013 08:09 Sujet du message: Posté le: 07/09/2013 08:09 Sujet du message: |
  |
|
|
Salut Fabrice !
Y'a ça qui peut t'aider :
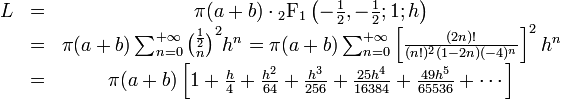
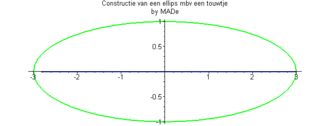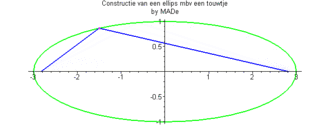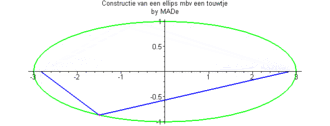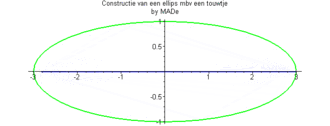
C'est simple....
Amicalement
Frédéric 


"L'eau plate ne favorise pas le vol de pente." Otto Lilienthal
"In Cyano véritas" Michel Coneuf
"Veni, bibi, vomi" Pasqual VOMITINO
Retroplane fort et vert ! |
|
| Revenir en haut de page |
|
 |
Tomek
Stagiaire Posteur


Inscrit le: 07 Sep 2013

Localisation: Marseille
Âge: 48

|
 Posté le: 07/09/2013 08:53 Sujet du message: Posté le: 07/09/2013 08:53 Sujet du message: |
  |
|
|
Bonjour Fabrice,
A mon avis c'est encore notre vieux Pythagore qui te donne la réponse:
(r-a)^2+c^2=r^2
Autrement dit r=(a^2+c^2)/2a
Amitiés,
Tomasz |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 07/09/2013 12:15 Sujet du message: Posté le: 07/09/2013 12:15 Sujet du message: |
  |
|
|
Heureusement qu'il y a les stagiaires posteurs pour proposer des solutions simples (à laquelle j'aurais dû penser, d'ailleurs...).
Moralité : plus on progresse dans l'ancienneté sur le forum, plus on invente des solutions abracadabrantesques! 
Merci Tomasz, surtout ne poste pas trop, pour rester dans le bas de l'ancienneté! 
Merci Marc, j'ai déjà téléchargé ce logiciel, mais il ne peut pas dessiner la partie basse du couple.
Et merci aux joyeux retro-men pour leurs solutions aussi diverses que faciles à mettre en oeuvre! 

Fabrice |
|
| Revenir en haut de page |
|
 |
Tomek
Stagiaire Posteur


Inscrit le: 07 Sep 2013

Localisation: Marseille
Âge: 48

|
 Posté le: 07/09/2013 12:39 Sujet du message: Posté le: 07/09/2013 12:39 Sujet du message: |
  |
|
|
![[good2]](images/smiles/good2.gif)
Tu peux compter la-dessus. Long chemin devant moi avant que j'ose poster plus sur ce forum  |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 17/09/2013 12:30 Sujet du message: Posté le: 17/09/2013 12:30 Sujet du message: |
  |
|
|
Chers mathématiciens rétroplanistes,
Je continue à me battre avec mes ellipses ; j'ai tracé tous les couples, j'en suis aux encoches des lisses.
Si on observe le schéma de principe en haut de page, on se rend compte qu'elles sont placées sur le pourtour du couple en fonction de la circonférence des parties cylindriques (y) et elliptiques (x).
Pour l'arc de cercle, pas de souci, Autocad me fournit la longueur de l'arc.
Pour l'arc d'ellipse, ça se complique : il n'y a pas de notion de longueur d'arc d'ellipse dans le clic droit du logiciel. Si le raccord entre le cercle et l'ellipse se situait à la moitié de l'ellipse, je n'aurais eu qu'à utiliser la formule qui donne (approximativement) la circonférence d'une ellipse, mais ce n'est pas le cas : sur le schéma, b et c sont différents!
Rassemblez vos neurones, affûtez vos formules et proposez-moi un moyen pour placer fidèlement ces ![[argh]](images/smiles/argh.gif) d'encoches... d'encoches...
Merci d'avance

Fabrice |
|
| Revenir en haut de page |
|
 |
Tomek
Stagiaire Posteur


Inscrit le: 07 Sep 2013

Localisation: Marseille
Âge: 48

|
 Posté le: 17/09/2013 13:13 Sujet du message: Posté le: 17/09/2013 13:13 Sujet du message: |
  |
|
|
Salut Fabrice,
Le raccord se fait exactement "à la moitié" de l'ellipse. Sinon le contour ne serait pas lisse à l'endroit du raccord ellipse-cercle. Le "c" n'a rien à voir la dedans. L'ellipse est définie par les valeurs "a" et "b". Le "c" te sert uniquement à tracer la partie inférieure du couple, il n'influe pas sur la partie elliptique du dessus.
En résumé, la longuer d'arc "x" vaut 1/4 de la circonférence de l'ellipse.
Après, je ne connais rien en cad donc je ne sais pas quel genre d'info il te faut pour que le logiciel trouve tes emplacements d'encoches.
A+,
Tomasz |
|
| Revenir en haut de page |
|
 |
Frédéric
Psycho Posteur


Inscrit le: 22 Juin 2006

Localisation: Corrèze
Âge: 61

|
 Posté le: 17/09/2013 13:44 Sujet du message: Posté le: 17/09/2013 13:44 Sujet du message: |
  |
|
|
Salut Fabrice !
Si tu regarde le joli gif animé au dessus, tu peux remarquer que la somme des longueur des deux segments qui fond le tour de l'ellipse et toujours égale... si ça peux aider...on ne sait jamais... en faisant des règles de trois pour placer les lisses sur les couples proportionnellement... ![[confus]](images/smiles/confus.gif)    
Amicalement
Frédéric 


"L'eau plate ne favorise pas le vol de pente." Otto Lilienthal
"In Cyano véritas" Michel Coneuf
"Veni, bibi, vomi" Pasqual VOMITINO
Retroplane fort et vert ! |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 17/09/2013 13:48 Sujet du message: Posté le: 17/09/2013 13:48 Sujet du message: |
  |
|
|
oui, mais non.
La circonférence totale est donnée par une intégrale, mais approchée par une formule plus simple qui ne fait intervenir que des racines, pi et des carrés 
Là où je bloque, c'est pour calculer une partie de cette circonférence...

Fabrice |
|
| Revenir en haut de page |
|
 |
Tomek
Stagiaire Posteur


Inscrit le: 07 Sep 2013

Localisation: Marseille
Âge: 48

|
 Posté le: 17/09/2013 18:22 Sujet du message: Posté le: 17/09/2013 18:22 Sujet du message: |
  |
|
|
Mais si je ne me trompe pas, la partie qu'il te faut c'est 1/4 de la circonférence, non? C'est cela le x sur le dessin.
Par contre, après il faut tracer les points qui correspondent à l'arc de longueur x/5, et là je ne sais pas comment faire géométriquement, même de manière approchée. Mais j'imagine que l'Autocad peut le faire numériquement avec une précision suffisante, une fois que tu connais la longueur de l'arc x. |
|
| Revenir en haut de page |
|
 |
ClaudeL
Accro Posteur


Inscrit le: 26 Jan 2006

Localisation: Vercors (FR)
Âge: 78

|
 Posté le: 17/09/2013 18:36 Sujet du message: Posté le: 17/09/2013 18:36 Sujet du message: |
  |
|
|
Salut les rétropythagoriciens,
Le calcul de la longueur d'un arc d'ellipse n'est pas du tout triviale et ne conduit pas à un résultat analytique rigoureux. Je pense que c'est surtout pour ça que les logiciels de DAO ne proposent pas de fonctions similaires à celles des cercles.
* Le plus simple sera de très loin
- 1) de calculer la longueur du 1/4 d'ellipse avec une quelconque formule d'approximation (Il y a du choix ici par exemple )
- 2) Reporter les longueurs des tronçons sur le dessin du couple avec réglet flexible !!
Si tu veux absolument avoir un dessin en DAO, tu peux toujours mesurer les positions angulaires des lisses par rapport au centre de l'ellipse et un axe de l'ellipse (rapporteur) et continuer ton dessin avec ton logiciel. |
|
| Revenir en haut de page |
|
 |
ClaudeL
Accro Posteur


Inscrit le: 26 Jan 2006

Localisation: Vercors (FR)
Âge: 78

|
 Posté le: 17/09/2013 20:37 Sujet du message: Posté le: 17/09/2013 20:37 Sujet du message: |
  |
|
|
Eh bien, une fois de plus, j'ai loupé une occasion de me taire !
Fabrice, tu as dans ton logiciel de DAO favori la fonction "diviser" qui fonctionne sur les lignes, cercles, ellipses, arcs... (je n'ai pas essayé avec les splines).
Dans ton cas de figure, tous les intervalles ne sont pas égaux : il y a des X/5 et des 2X/15. Tu divises le 1/4 d'ellipse par 15 et tu ne gardes que les points intermédiaires qui te conviennent. |
|
| Revenir en haut de page |
|
 |
de plancke
Incurable Posteur


Inscrit le: 18 Fév 2009

Localisation: martigues
Âge: 50

|
|
| Revenir en haut de page |
|
 |
VincentB
Serial Posteur


Inscrit le: 23 Jan 2006

Localisation: Lanzarote - Charco del Palo
Âge: 62

|
 Posté le: 18/09/2013 05:16 Sujet du message: Posté le: 18/09/2013 05:16 Sujet du message: |
  |
|
|
« de plancke » a écrit: Bon je suis sur autocad et je ne trouve pas la fonction diviser ![[humm]](images/smiles/humm.gif)
Dessin > Point > Diviser ou tu tapes "diviser" ou "_divide" et pour visualiser les points, changer leur style
Format > style de points >...
« ClaudeL » a écrit: ... la fonction "diviser" qui fonctionne sur les lignes, cercles, ellipses, arcs... (je n'ai pas essayé avec les splines).
c'est bon aussi avec les splines
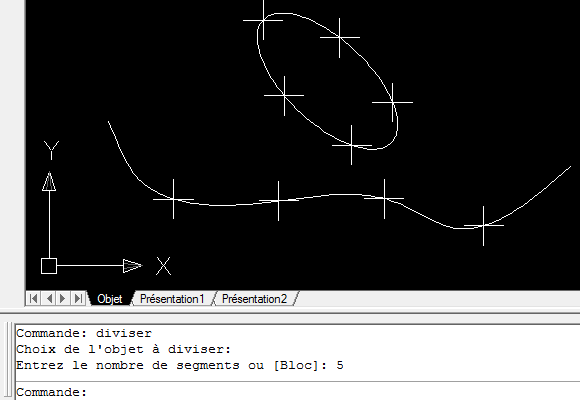

Retroplane et modélisme en pause, vanlife à haute dose.
|
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 18/09/2013 06:53 Sujet du message: Posté le: 18/09/2013 06:53 Sujet du message: |
  |
|
|
Comme un boulet, je n'avais pas pensé à la fonction "diviser", que je connais pourtant... 
Tomek : s'il avait fallu diviser l'ellipse en 4, ç'aurait été trop simple ; la partie elliptique du couple ne représente pas un quart.
J'essaie cette miraculeuse fonction de division à la pause de midi.
Merci à vous, ô grands Euler, Thalès et Poincaré que vous êtes! 

Fabrice |
|
| Revenir en haut de page |
|
 |
Tomek
Stagiaire Posteur


Inscrit le: 07 Sep 2013

Localisation: Marseille
Âge: 48

|
 Posté le: 18/09/2013 07:34 Sujet du message: Posté le: 18/09/2013 07:34 Sujet du message: |
  |
|
|
Bon, je suis têtu donc je soutiens toujours que la partie supérieure de ton couple correspond à la moitié de l'ellipse, et donc l'arc x en représente un quart. Après, comme c'était déjà dit, il faut diviser (numériquement) ce quart en 15 parties égales et ne prendre en compte que certains points de cette division.
Mais peut-être tu as interprété le dessin initial autrement et les couples que tu as tracé ne sont pas faites de moitié d'ellipse, d'où la confusion ?
Bonne journé,
Tomasz |
|
| Revenir en haut de page |
|
 |
Orionis
Incurable Posteur


Inscrit le: 31 Aoû 2006

Localisation: Drôme
Âge: 59

|
 Posté le: 18/09/2013 20:42 Sujet du message: Posté le: 18/09/2013 20:42 Sujet du message: |
  |
|
|
Tomek, tu as bien fait d'être têtu, tu as raison.  

Fabrice |
|
| Revenir en haut de page |
|
 |
|

